信息的存储

字节：大多数计算机都使用字节(byte)作为系统中最小内存单位，内存就可以看作一个巨大的byte数组

虚拟地址空间：操作系统为程序提供虚拟内存(virtual memory)这一概念屏蔽了底层存储系统的复杂性，其中虚拟内存中每个字节都有自己的地址，也就是虚拟地址(virtual address)，虚拟内存中所有可能地址的集合就是虚拟地址空间(virtual address space)，C语言中某个指针的值就是某个存储块第一个字节的虚拟地址

指针：C语言的重要特性，有值和类型两个属性，值是某个对象的虚拟地址，类型是表示那个位置上存储对象的类型

十六进制

一个字节是8位，表示成二进制是00000000 ~ 11111111，表示成十进制的范围是0 ~ 255，表示成十六进制是00 ~ FF，很明显十六进制的表示方式更加简洁易用，计算机系统中通常以0x开头表示一个以十六进制展现的内存地址

字长

所谓字长，就是指针携带的地址值的标称大小，32位字长的机器其虚拟地址范围就是0 ~ 2^32^（最大虚拟地址值是2^32^-1，也就是说32位字长的系统虚拟地址空间大小就是4GB），64位字长的机器其虚拟地址范围就是0 ~ 2^64^（16EB）

向后兼容：64位机器可以运行32位机器编译的程序，但32位机器无法运行64位机器编译的程序

寻址

一个对象在内存中是以连续的字节序列的形式存储的，对象的地址就是这段字节序列中最低位置的地址值

对象字节序列中，开始位置的字节称为最低有效位，结束位置称为最高有效位，比如对于0x01234567这个int，最高有效位字节就是01，最低有效位字节是67

字节顺序

对象在内存中的字节序列是由一定的顺序进行保存的，保存对象字节序列的顺序就是字节顺序，有大端法和小端法两种：

  • 大端法：从最高有效位到最低有效位的顺序存储对象
  • 小端法：从最低有效位到最高有效位的顺序进行存储
字符串的字节顺序

字符串类型的字节顺序与其他类型稍有不同，在任意平台上字符串都是正序排列

布尔代数

布尔运算在计算机系统中占有很重要的地位，在数值位运算中运用尤为广泛

基本的布尔运算逻辑有四种&（与），|（或），~（非），^（异或），四种布尔运算逻辑表格如下：

img

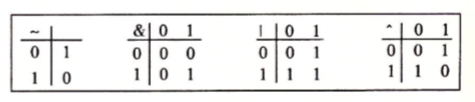
位运算

布尔代数在计算机科学中一个很重要的运用就是位运算，C和Java等高级语言都支持位运算

有以下程序，可以将x和y各自的地址相互对调：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
void inplace_swap(int *x, int *y) {
    *y = *x ^ *y;
    *x = *x ^ *y;
    *y = *x ^ *y;
}
int main() {
    int x = 10;
    int y = 9;
    inplace_swap(&x, &y);
    printf("%d\n", x);
    printf("%d", y);
    return 0;
}

打印结果显示x=9，y=10，因为我们通过三次异或运算将x和y的值进行了对调，由此产生了一些结论：

  1. 异或运算中，任何值与0的异或结果还是它本身
  2. 异或运算中，任何值与它自己的异或结果为0
  3. 异或运算支持结合律

通过以下函数可以将一个数组前后颠倒：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void reverse_array(int a[], int count) {
    int first, last;
    for (first = 0, last = count -1; first < last; first++, last--) {
        inplace_swap(&a[first], &a[last]);
    }
}
int main() {
    int a[] = {1, 2, 3, 4, 5, 6};
    int len = sizeof(a) / sizeof(a[0]);
    printf("size of array is %d\n", len);
    reverse_array(a, len);
    for (int i = 0; i < len; i++) {
        printf("%d\n", a[i]);
    }
    return 0;
}

打印结果是”6, 5, 4, 3, 2, 1”

逻辑运算符

逻辑运算符和位运算符功能相似，不过逻辑运算符针对Boolean类型，而位运算符仅仅对数字做二进制位运算

移位运算

移位运算通常用于对数字的二进制位进行移动计算，具体的移位运算还包括逻辑移位和算术移位：

img

与逻辑右移位不同的是，算术右移位会在空出来的高位补足移位个数的最高有效位的值

与C语言不同的是，Java中>>代表算术右移位，>>>代表逻辑右移位

注意：移位运算符的优先级低于加减法运算符

整数表示

整数类型在32位机器和64位机器上的取值范围是不一样的，int类型都是4字节编码，long类型在32位机器上是4字节编码，在64位机器上是8字节编码，此外C语言规定int类型可以用2字节长度来编码，long字节可以用4字节长度来编码，我想这应该是为了兼容32位和64位的平台

无符号数

无符号数是没有负数编码的数字，最小值为0，在C语言中用unsigned进行声明，一般来说int表示有符号整形，uintb表示无符号整形 （与C语言不同，Java没有无符号数）

无符号数编码唯一性：在计算机系统中无符号数的编码具有唯一性，比如无符号数10的二进制编码是1010，那么可以断言1010这个编码如果表示的是一个无符号数的话，那它对应的十进制就只能是10

有符号数

学习有符号数前需要先了解补码编码

补码编码

补码`是计算机系统中表示负数必不可少的编码手段，通过补码表示的数字的最高有效位是符号位，为0则表示正数，为1则表示负数

补码转换为十进制有符号数：以下是换算补码二进制数到十进制数的两种方式：

权重法：换算方式与无符号二进制转十进制的方式类似，不过高位符号位需要取负号：
$$
1011: -1 2^3 + 0 2^2 + 1 2^1 + 1 2^0 = -5
$$

$$
0101: 0 2^3 + 1 2^2 + 0 2^1 + 1 2^0 = 5
$$

取反法：判断最高有效位，如果最高位为0，则为正数，计算方式与无符号数一致，如果为1，则为负数，将最高位去掉，剩余位减去1后各位再取反，得到的二进制编码则是该负数的绝对值，比如上述例子中的1011去掉最高位后未011，减去1后为010，全部取反后为101，转换为十进制为5，则该负数是-5

十进制有符号数转换为补码: 相应的，将十进制负数-5转换为补码形式1011就有以下方式

1
2
3
4
# 绝对值转换为二进制： 101
# 二进制位全部取反： 010
# 加1： 011
# 加上符号位： 1011

整数运算

无符号加法

使用无符号加法需要注意溢出的情况，下列无符号short求和最后结果就发生了溢出，同样产生了截断，实际结果比理想的结果少了2^16^

1
2
unsigned short c = 44444 + 22222;
printf("a is %u, b is %u, result is %u", a, b, c);

最后结果为1130，想要的结果是66666

补码加法

大部分时间进行数值计算都是对补码进行操作，在进行补码加法时需要考虑当结果太大或者太小时会不会发生溢出的情况

与无符号加法类似，如果加法结果超过当前数值类型的位数范围时会发生正溢出（太大）或者负溢出（太小）：

img

1
2
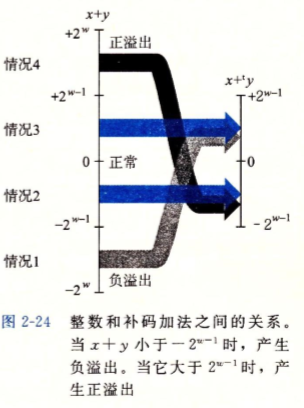
short c = -22222 + (-22222);
printf("a is %u, b is %u, result is %u", a, b, c);

其结果为21092，发生了负溢出，其结果比想要的结果大了65536，也就是2^16^

以下函数无法判断两个有符号补码数相加是否发生了溢出：

1
2
3
4
int check_overflow_short_add(int a, int b) {
    int c = a + b;
    return (c - a) == b && (c - b) == a;
}

两个补码a和b相加得到结果c，不管有没有溢出，c-a的结果始终还是b，c-b的结果始终还是a

无符号乘法

无符号乘法也存在高位截断的问题：

1
2
3
4
unsigned short a = 222;
unsigned short b = 333;
unsigned short c = a * b;
printf("%d", c);

理想结果为73926，实际得到的结果为8390，说明溢出的部分被截断了，只剩下了低16位的数据，也就是少了2^16^

补码乘法

补码乘法与无符号乘法差不多(两者的乘法运算位级表示都一样)，与补码加法一样也需要注意正溢出和负溢出截断的问题

对于某些常数乘法的优化

乘法运算在大多数计算机上都是一个相当慢的运算，需要消耗过多的时钟周期，因此编译器对常数乘法运算会进行一些优化，用移位或者加法运算来代替常数因子的乘法运算

移位优化：某个数与2的幂作乘法就可以进行移位运算，X * 2^k就可以直接将X左移k位

加法优化：将乘数拆散为2的幂次的和，比如X * 14就可以拆为X * (2^3 + 2^2 + 2)，然后再用移位计算各个部分的值，最后再统一相加

浮点数

现代计算机采用IEEE浮点数标准来处理带小数点的数字

二进制表示小数

与整数的二进制表示法类似，带小数的数字是用2的负幂次叠加来进行表示，比如5.75就可以拆散为：

4 + 0 + 1 + 1/2 + 1/4，用二进制进行表示就是：101.11

二进制用以下规则表示带小数的数字，整数部分就是2的正幂次，小数部分就是2的负幂次：

img

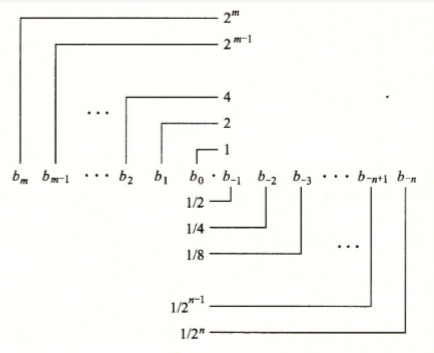
缺陷：可以看出，二进制表示小数无法做到像十进制这么精确，像1/5这种小数通过十进制可以表示为0.2，但是用二进制的话只能通过增加二进制小数位数构造一个近似值来逼近，例如0.00110011这个二进制小数转换为十进制是0.19921875，已经很接近了

IEEE浮点数表示法

在二进制定点表示法的基础上，IEEE标准用以下公式来存储一个浮点数：

img

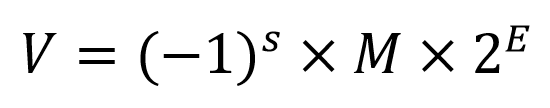
各个参数解释如下：

  • s：符号标记，无论是float还是double类型都是有符号数，s为1则表示负数，s为0表示正数
  • M：尾数，保存浮点数的实际有效位，其大小是1 <= M < 2，以1.1101这样的形式展示；不过存储的时候会省略小数点左边的1，只存储右边的位，我们把保留下来的小数点右边的位称为f
  • E：阶码，对尾数M进行加权，判断M的小数点需要左移或者右移多少位，最终计算得到真正的浮点数二进制表示

计算机系统保存浮点数就是对这三个参数分别进行编码保存到固定的位数中，float类型保存到32位长度中，double类型则保存到64位长度中

float & double：单精度浮点（float）和双精度浮点（double）除了最高位的符号位s，剩下的区别主要体现在对M和E的保存位数不一样：

  • float：E取8位，M取23位
  • double：E取11位，M取52位

以32位的float为例讲一下编码保存各个参数的规则：

  • 编码s：保存为1或者0
  • 编码E：E的值即要表现2的正幂次，也要表现2的负幂次，而编码保存后的八位数e只能是无符号整数，范围是0 ~ 2^8^-1=255，因此E的真实取值范围需要在这个基础上做一个2^7^-1=127的偏移处理，也就是说e = E + 127
  • 编码M：省略掉M小数点左边的1，只保留小数点右边的23位，也就是f

基于这个基本表示规则，有四种不同的情况，以32位float为例：

  • E编码保存的值(e)不为0或者255(2^8-1)：这种情况即为普通情况，E的取值范围是-126 ~ 127
  • e所有位都为0：称为非规格化值，规定这种情况在解码时舍弃掉M小数点左边的1，只保留f；这种情况一般时拿来表示正0或者负0，或者非常逼近于0的小数
  • e所有位都为1 & f所有位为0：无穷大数，s为1是负无穷，s为0是正无穷
  • e所有位都为1 & f不为0：NaN，用来表现不是数字（无意义的数字）的情况

例子：以float类型1.25为例，计算机系统中使用32位二进制00111111101000000000000000000000来保存1.25

img

如图：

  1. 符号位s为0，表示正数
  2. 阶码位e有8位，其值是127，因此E = 127 - 127 = 0，阶码E为0
  3. 尾数位f有23位，其值是二进制0.01，也就是1/(2^2) = 1/4

最终值V = 1 * (1/(2^2)) * 1 = 1.25