连续物理内存分配综述
基本要求:一个进程需要一块存储时分配,完成工作后收回
基本结构:首先分为物理存储和逻辑存储。
物理存储可以从计算机体系结构的三个重要模块入手:CPU、内存和IO
我们可以将各个部分以存储为逻辑,做层次化的区分:
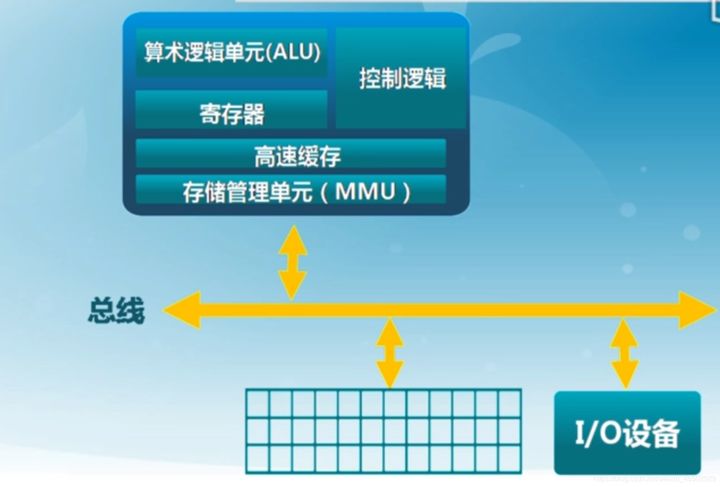
大体的调用关系如下,首先要考虑最为快速的缓存,其存取速度与CPU主频相同。缓存的使用是我们所不能意识到的,因为其依靠硬件实现。但内存和外存是我们需要在操作系统当中操作的。
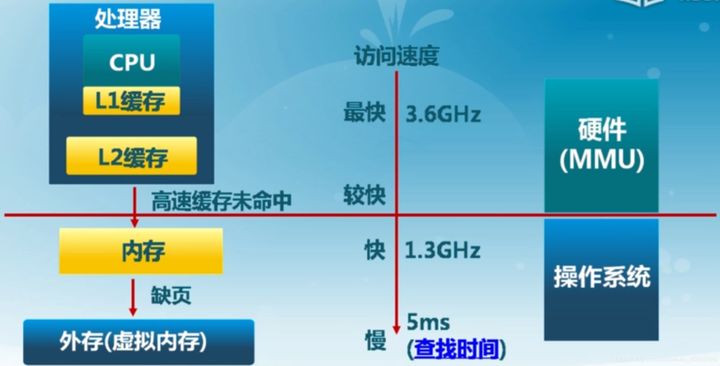
逻辑地址空间:物理地址如果交由计算机或许是可以方便使用的,但是对于人来说,并不容易记忆理解和使用。我们希望我们各个进程使用的存储都相对性地低耦合,有一个比较清晰的逻辑结构。把线性的物理地址编号转换为抽象的逻辑内存结构的计算机硬件是MMU(Memory Management Unit)
内存管理的核心目的:抽象(逻辑地址空间)、保护(独立地址空间)、共享(访问相同内存)、虚拟化(更大的地址空间)
实现方法:重定位(relocation)、分段(segmentation)、分页(paging)、虚拟存储(virtual memory)
地址空间和地址生成
地址空间的定义
物理空间地址:硬件支持的地址空间,起始地址为0,直到MAXsys
逻辑地址空间:在CPU运行的进程看到的地址,起始地址同样为0,直到MAXprog
逻辑地址的生成
主要步骤:编译、汇编、链接、重定位
地址生成的时机和限制
- 如果起始地址已知,则地址在编译时生成,起始地址改变必须重新编译
- 编译时起始位置未知,编译器需要生成可重定位的代码,加载时生成绝对地址
- 也可以在执行时生成地址,执行时代码可移动,需地址转换硬件支持
不同的系统里,这几种方法均有采用
地址生成过程
ALU(算术逻辑单元)所需要的地址是逻辑地址,但向内存中取用时,需要的是物理地址。
CPU中依靠MMU进行一次逻辑到物理地址的转换。虽然这是硬件完成的,但是操作系统提供两者之间的关系的描述(这是页表的功劳)
而后还要进行地址检查,防止超过段长度。加上段基址完成重定位即可。
连续内存分配算法
几个概念
- 连续内存分配:给进程分配一块不小于指定大小的连续物理内存区域。
- 内存碎片:不能被利用的空闲内存
- 外部碎片:分配单元之间的未被利用内存
- 内部碎片:分配单元内部的未被使用内存,取决于分配单元大小是否要取整
动态分配策略
最先分配策略:(first-fit)
- 空闲分区列表按地址大小排序,直接选用第一个够用的分区。
- 优点:简单,且高地址处会有大块的分区
- 缺点:是会产生外碎片,且分配大块时需要搜索较长时间
最优分配策略(best-fit):
- 申请:空闲分区列表从小到大排序,搜索一个比它大但最小的分区,分区利用率最高
- 释放:释放时要在空闲分区中查找相邻空闲分区,较慢
- 外碎片:避免大分区拆分,减小外碎片大小,简单,但同时外碎片难以利用
最差分配策略:
- 与最优策略对应,空闲分区由大到小排。找一个能容纳它的最大空闲分区(即从头开始搜索时找到的第一个大于它的空闲分区)
- 优点:中等大小分配较多时效果较好,避免出现太多的小碎片
- 缺点:释放空间较慢;大分区被破坏掉,而后难以分配较大的空间
碎片整理算法
通过调整进程占用的分区位置来减少或者避免分区碎片
紧凑:
- 定义:通过移动分配给进程的内存分区,以合并外部碎片
- 条件:所有的应用可以动态重定位
- 问题:进程等待时移动。开销
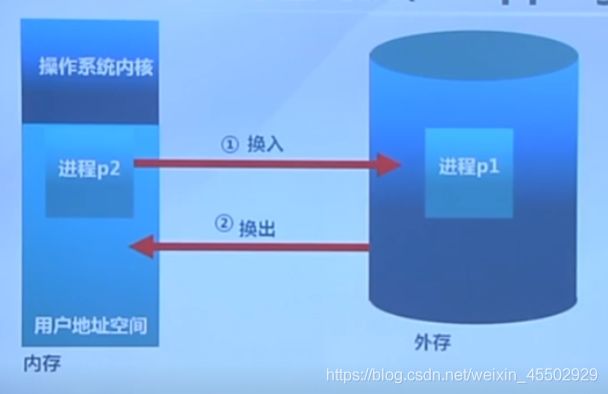
分区对换:
- 定义:通过抢占并回收处于等待状态进程的分区,从而增大可用内存空间。
- 类似windows的虚拟内存机制,相等于将一部分外存用作内存,.swp文件就来源于分区对换(swapping)
- 早期多进程实现方式
伙伴系统
伙伴系统(buddy system)就是采用二分的思路进行占用率相对较高的分配。
分配时:
- 所有可分配的空闲分区大小都为2的幂
- 如果整个可分配分区的大小为$2^k$,且需要分配的分区大小$2^{k-1} \leq s \leq 2^k$,那么就将这个分区整个分配。如果不够继续二分,递归至超过50%利用率。
释放时:
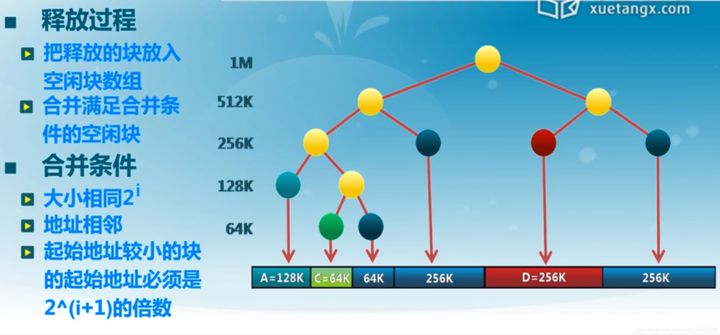
合并时注意,两段内存可以合并的条件是,它们两个对应的节点在二叉树中的父节点相同。(即合并条件的最后一条)
分配释放示例如下:
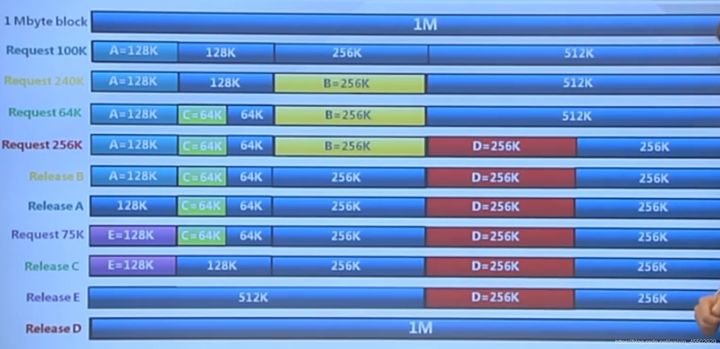
相关题目
- 在启动页机制的情况下,在CPU运行的用户进程访问的地址空间是(逻辑地址空间)
- 在使能分页机制的情况下,不会产生外碎片
- 操作系统中可采用的内存管理方式包括重定位(relocation)、分段(segmentation)、分页(paging)、段页式(segmentation+paging)
