差分隐私

概念

差分隐私，英文名为differential privacy，顾名思义，保护的是数据源中一点微小的改动导致的隐私泄露问题。比如有一群人出去聚餐，那么其中某人是否是单身狗就属于差分隐私。

为了更形式化地描述差分隐私，我们需要先定义相邻数据集。现给定两个数据集D和D’, 若它们有且仅有一条数据不一样，那我们就称此二者为相邻数据集。以上面数据集为例：假定有 $n$ 个人，他们是否是单身狗，形成一个集合 $\{a_1,a_2, …, a_n\}$ （其中 $a_i = 0$ 或 $1$ ），那么另一个集合当中只有一个人改变了单身状态，形成另一个集合 $\{a_1’, a_2’, …, a_n’\}$ ，也就是只存在一个 $i$ 使得 $a_i \ne a_i’$ ，那么这两个集合便是相邻集合。

那么对于一个随机化算法 $A$ （所谓随机化算法，是指对于特定输入，该算法的输出不是固定值，而是服从某一分布），其分别作用于两个相邻数据集得到的两个输出分布难以区分。差分隐私形式化的定义为：

$Pr\{A(D) = O\} ≤e^\epsilon \cdot Pr\{A(D’) = O\}$

也就是说，如果该算法作用于任何相邻数据集，得到一个特定输出 $O$ 的概率应差不多，那么我们就说这个算法能达到差分隐私的效果。也就是说，观察者通过观察输出结果很难察觉出数据集一点微小的变化，从而达到保护隐私的目的。

如何实现

那如何才能得到差分隐私呢？最简单的方法是加噪音，也就是在输入或输出上加入随机化的噪音，以期将真实数据掩盖掉。比较常用的是加拉普拉斯噪音（Laplace noise）。由于拉普拉斯分布的数学性质正好与差分隐私的定义相契合，因此很多研究和应用都采用了此种噪音。还是以前面那个数据集为例，假设我们想要知道到底有多少人是单身狗，我们只需要计算 $\sum a_i$ ，那么为了掩盖具体数值，实际输出值应为 $O=\sum a_i r_{lap}$ ，相应地，另一个数据集输出的是 $O’= \sum a_i’ r_{lap}’$ 。这使得观察者分不清最终的输出是由哪个数据集产生的。

前面描述的是差分隐私的严格定义。还有一种稍微放宽一点的定义为：

$Pr\{A(D) = O\} \le e^\epsilon \cdot Pr\{A(D’) = O\} \delta$

其中 $\delta$ 是一个比较小的常数。要获取这种差分隐私，我们可以使用高斯噪音（Gaussian noise）。

当然，对输入或输出加噪音会使得最终的输出结果不准确。而且由于噪音是为了掩盖一条数据，所以很多情况下数据的多少并不影响加的噪音的量。那么在数据量很大的情况下，噪音的影响很小，这时候就可以放心大胆地加噪音了，但数据量很小的情况下，噪音的影响就显得比较大，会使得最终结果偏离准确值较远而变得不可用。也有些算法不需要加噪音就能达到差分隐私的效果，听起来很美好，但这种算法通常要求数据满足一定的分布，这一点在现实中通常很难满足。

本地化差分隐私和中心化差分隐私的区别

中心化差分隐私与本地化差分隐私主要的区别在于处理过程的不同。中心化差分隐私对采集后的数据进行扰动，因此需要一个可信的中心服务进行数据的汇总和处理；而本地化差分隐私在数据的源头进行扰动保护，因此允许数据拥有者在本地进行处理，更好地保护了隐私。

同态加密

什么是同态加密？

提出第一个构造出全同态加密（Fully Homomorphic Encryption）[Gen09]的Craig Gentry给出的直观定义最好：

A way to delegate processing of your data, without giving away access to it.

这是什么意思呢？一般的加密方案关注的都是数据存储安全。即，我要给其他人发个加密的东西，或者要在计算机或者其他服务器上存一个东西，我要对数据进行加密后在发送或者存储。没有密钥的用户，不可能从加密结果中得到有关原始数据的任何信息。只有拥有密钥的用户才能够正确解密，得到原始的内容。我们注意到，这个过程中用户是不能对加密结果做任何操作的，只能进行存储、传输。对加密结果做任何操作，都将会导致错误的解密，甚至解密失败。

同态加密方案最有趣的地方在于，其关注的是数据处理安全。同态加密提供了一种对加密数据进行处理的功能。也就是说，其他人可以对加密数据进行处理，但是处理过程不会泄露任何原始内容。同时，拥有密钥的用户对处理过的数据进行解密后，得到的正好是处理后的结果。

有点抽象？我们举个实际生活中的例子。有个叫Alice的用户买到了一大块金子，她想让工人把这块金子打造成一个项链。但是工人在打造的过程中有可能会偷金子啊，毕竟就是一克金子也值很多钱的说… 因此能不能有一种方法，让工人可以对金块进行加工（delegate processing of your data），但是不能得到任何金子（without giving away access to it）？当然有办法啦，Alice可以这么做：

Alice将金子锁在一个密闭的盒子里面，这个盒子安装了一个手套。
工人可以带着这个手套，对盒子内部的金子进行处理。但是盒子是锁着的，所以工人不仅拿不到金块，连处理过程中掉下的任何金子都拿不到。
加工完成后。Alice拿回这个盒子，把锁打开，就得到了金子。

这里面的对应关系是：

盒子：加密算法
盒子上的锁：用户密钥
将金块放在盒子里面并且用锁锁上：将数据用同态加密方案进行加密
加工：应用同态特性，在无法取得数据的条件下直接对加密结果进行处理
开锁：对结果进行解密，直接得到处理后的结果

同态加密哪里能用？

这几年不是提了个云计算的概念嘛。同态加密几乎就是为云计算而量身打造的！我们考虑下面的情景：一个用户想要处理一个数据，但是他的计算机计算能力较弱。这个用户可以使用云计算的概念，让云来帮助他进行处理而得到结果。但是如果直接将数据交给云，无法保证安全性啊！于是，他可以使用同态加密，然后让云来对加密数据进行直接处理，并将处理结果返回给他。这样一来：

用户向云服务商付款，得到了处理的结果；
云服务商挣到了费用，并在不知道用户数据的前提下正确处理了数据；

这方法简直完美啊有没有？！但是，这么好的特性肯定会带来一些缺点。同态加密现在最需要解决的问题在于：效率。效率一词包含两个方面，一个是加密数据的处理速度，一个是这个加密方案的数据存储量。我们可以直观地想一想这个问题：

工人戴着手套加工金子，肯定没有直接加工来得快嘛~ 也就是说，隔着手套处理，精准度会变差（现有构造会有误差传递问题），加工的时间也会变得更长（密文的操作花费更长的时间），工人需要隔着操作，因此也需要更专业（会正确调用算法）。
金子放在盒子里面，为了操作，总得做一个稍微大一点的盒子吧，要不然手操作不开啊（存储空间问题）。里面也要放各种工具吧，什么电钻啦，锉刀啦，也需要空间吧？

K匿名算法

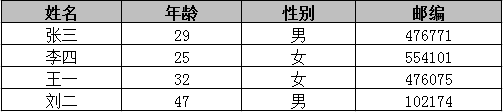
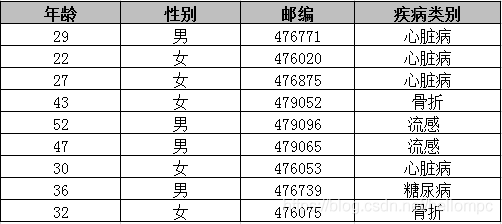
在大数据的时代，很多机构需要面向公众或研究者发布其收集的数据，例如医疗数据，地区政务数据等。这些数据中往往包含了个人用户或企业用户的隐私数据，这要求发布机构在发布前对数据进行脱敏处理。K匿名算法是比较通用的一种数据脱敏方法。举例来说，如下图是两张表，一张是用户的会员注册信息表，一张是对外发布的医疗信息表。

第二张医疗信息表中，虽然已经把用户姓名，身份证号等个人关联信息抹去，但如果直接发布这样简单匿名处理的数据，同样会带来数据泄露的风险。因为通过两张不同数据来源的表进行关联，对出生日期，性别，邮编的值进行匹配，可以定位出张三患有心脏病的隐私数据。这种通过某些属性与外部表链接的攻击称为链接攻击。

如上图两个表所示，每一行代表用户的一条记录，每一列表示一个属性。每一个记录与一个特定的用户/个体关联，这些属性可以分为三类：

标识符(Explicit Identifier)：可以直接确定一个个体，如：身份证号，姓名等。
准标识符集(Quasi-identifier Attribute set): 可以和外部表链接来识别个体的最小属性集，如：邮编，生日，性别等。
敏感数据(Sensitive Attributes)：用户不希望被人知道的数据，如：薪水，疾病历史，购买偏好等。

K-匿名(K-Anonymity)是Samarati和Sweeney在1998年提出的技术，该技术可以保证存储在发布数据集中的每条个体记录对于敏感属性不能与其他的K-1个个体相区分，即K-匿名机制要求同一个准标识符至少要有K条记录，因此观察者无法通过准标识符连接记录。

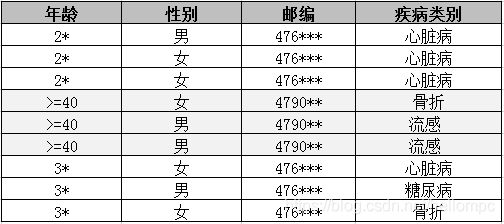
K-匿名的具体使用如下：隐私数据脱敏的第一步通常是对所有标识符列进行移除或是脱敏处理，使得攻击者无法直接标识用户。但是攻击者还是有可能通过多个准标识列的属性值识别到个人。攻击者可能通过（例如知道某个人的邮编，生日，性别等）包含个人信息的开放数据库获得特定个人的准标识列属性值，并与大数据平台数据进行匹配，从而得到特定个人的敏感信息。为了避免这种情况的发生，通常也需要对准标识列进行脱敏处理，如数据泛化等。数据泛化是将准标识列的数据替换为语义一致但更通用的数据，以上述医疗数据为例，对邮编和年龄泛化后的数据如下图所示。

经过泛化后，有多条纪录的准标识列属性值相同。所有准标识列属性值相同的行的集合被称为相等集。K-匿名要求对于任意一行纪录，其所属的相等集内纪录数量不小于K，即至少有K-1条纪录的准标识列属性值与该条纪录相同。

K-匿名技术就是每个相等集(或称为等价组)中的记录个数为K个，那么当针对大数据的攻击者在进行链接攻击时，对于任意一条记录的攻击同时会关联到相等集中的其他K-1条记录。这种特性使得攻击者无法确定与特定用户相关的记录，从而保护了用户的隐私。

K-匿名技术能保证以下三点：

攻击者无法知道某特定个人是否在公开的数据中
给定一个人，攻击者无法确认他是否有某项敏感属性
攻击者无法确认某条数据对应的是哪个人

但从另外一个角落来看，K-匿名技术虽然可以阻止身份信息的公开，但无法防止属性信息的公开，导致其无法抵抗同质攻击，背景知识攻击，补充数据攻击等情况：

同质攻击: 如在上面的K-匿名医疗信息表中，第1-3条记录的敏感数据是一致的，因此这时候K-匿名就失效。观察者只要知道表中某一个用户的邮编是476***，年龄在20多岁，就可以确定他有心脏病。
背景攻击: 如果观察者通过邮编和年龄确定用户王一在K-匿名医疗信息表的等价集3中，同时观察者知道王一患心脏病的可能很小，那么他就可以确定王一曾经骨折。

补充数据攻击：当公开的数据有多种类型，如果他们的K-匿名方法不同，那么攻击者可以通过关联多种数据推测用户信息。

L多样化

什么是L多样化

为了解决同质性攻击和背景知识攻击所带来的隐私泄露，Machanavajjhala等人提出了L-多样性(l-diversity)模型。简单来说，就是在公开的数据中，每一个等价类里的敏感属性必须具有多样性，即L-多样性保证每一个等价类里，敏感属性至少有L个不同的取值，通过这样L-多样性使得攻击者最多只能以1/L的概率确认某个体的敏感信息，从而保证用户的隐私信息不能通过背景知识，同质知识等方法推断出来。

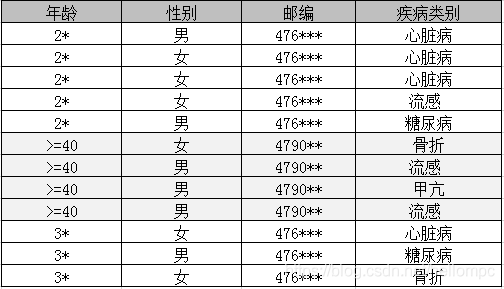
如上图所示，在每一个等价集中，包含至少3个以上不同的属性值，那么这部分公开数据就满足3-diversity的属性。

要实施L-多样性模型，除了上述的不可区分属性方式，通常还可以引入其他的统计方法来实现：

不可区分L-多样性(Distinction L-Diversity): 在同一个等价类中至少出现L个不同的敏感属性值。

基于概率的L-多样性(Probabilistic L-Diversity)：在一个类型中出现频率最高的值的概率不大于1/L；

基于熵的L-多样性(Entropy L-Diversity): 在一个等价类中敏感数据分布的熵至少是log(L)；

递归(C,L)-多样性(Recursive (C,L)-Diversity): 通过递归的方式，保证等价类中最经常出现的值的出现频率不要太高。

递归(C1, C2, L)-多样性(Recursive(C1,C2,L)-Diversity): 通过递归的方式，保证等价类中最经常出现的值的出现频率不要太高, 同时还保证了等价类中频率最低的敏感属性出现的频率不能太低。

L-多样性也具有一定局限性

敏感属性比例的严重不均衡导致L-多样性难以实现，例如某疾病检测报告，敏感属性只有“阳性”和“阴性”，分别占比1%和99%，阴性人群并不在乎被人知道结果，但阳性人群可能很敏感。如果在一个等价类中均为阴性，是没有必要实现可区分的2-Diversity。
偏斜性攻击(Skewness Attack)：如果在上面那个例子中，我们保证了阳性和阴性出现的概率相同，虽然保证了多样性，但是泄露隐私的可能性会变大，因为L-多样性并没有考虑敏感属性的总体分布。

L-多样性没有考虑敏感属性的语义，而导致敏感信息的泄露。例如敏感属性是“工资”，某一等价类中的取值全为2K-3K之间，那么观察者只要知道用户在这一等价类就可以知道其工资处于较低水平，具体数值观察者并不关心。

安全多方计算（MPC）

安全多方计算（Secure Muti-party Computation，简称MPC，亦可简称SMC或SMPC）问题首先由华裔计算机科学家、图领奖获得者姚期智教授于1982年提出，也就是为人熟知的百万富翁问题：两个争强好胜的富翁Alice和Bob在街头相遇，如何在不暴露各自财富的前提下比较出谁更富有？

简单来说，安全多方计算协议作为密码学的一个子领域，其允许多个数据所有者在互不信任的情况下进行协同计算，输出计算结果，并保证任何一方均无法得到除应得的计算结果之外的其他任何信息。换句话说，MPC技术可以获取数据使用价值，却不泄露原始数据内容。

可验证计算（Verifiable Computing）

可验证计算通常是指Verifiable Computing(简称“VC”)，指可以将计算任务外包给第三方算力提供者；（不受信任的）第三方算力提供者需要在完成计算任务的同时，提交一份关于计算结果的正确性证明。